In our latest release, version 1.11.8.27, we now support GPT and Transformer Models based on the open source minGPT GitHub project by Karpathy [1].
GPT uses transformer models to learn the context of the input data via attention layers. Stacking up a set of transformer blocks tends to learn context at several different levels from the training input. For more information on the minGPT project either see the Karpathy GitHub Site or check out our previous blog post minGPT – How It Works.
GPT MyCaffe Model
Implementing GPT in MyCaffe required creating several new layers: TransformerBlockLayer, CausalSelfAttentionLayer, LayerNormLayer, SoftmaxCrossEntropy2Layer, TokenizedDataLayer, and a new AdamWSolver [2]. Used together, these form the minGPT model shown below.
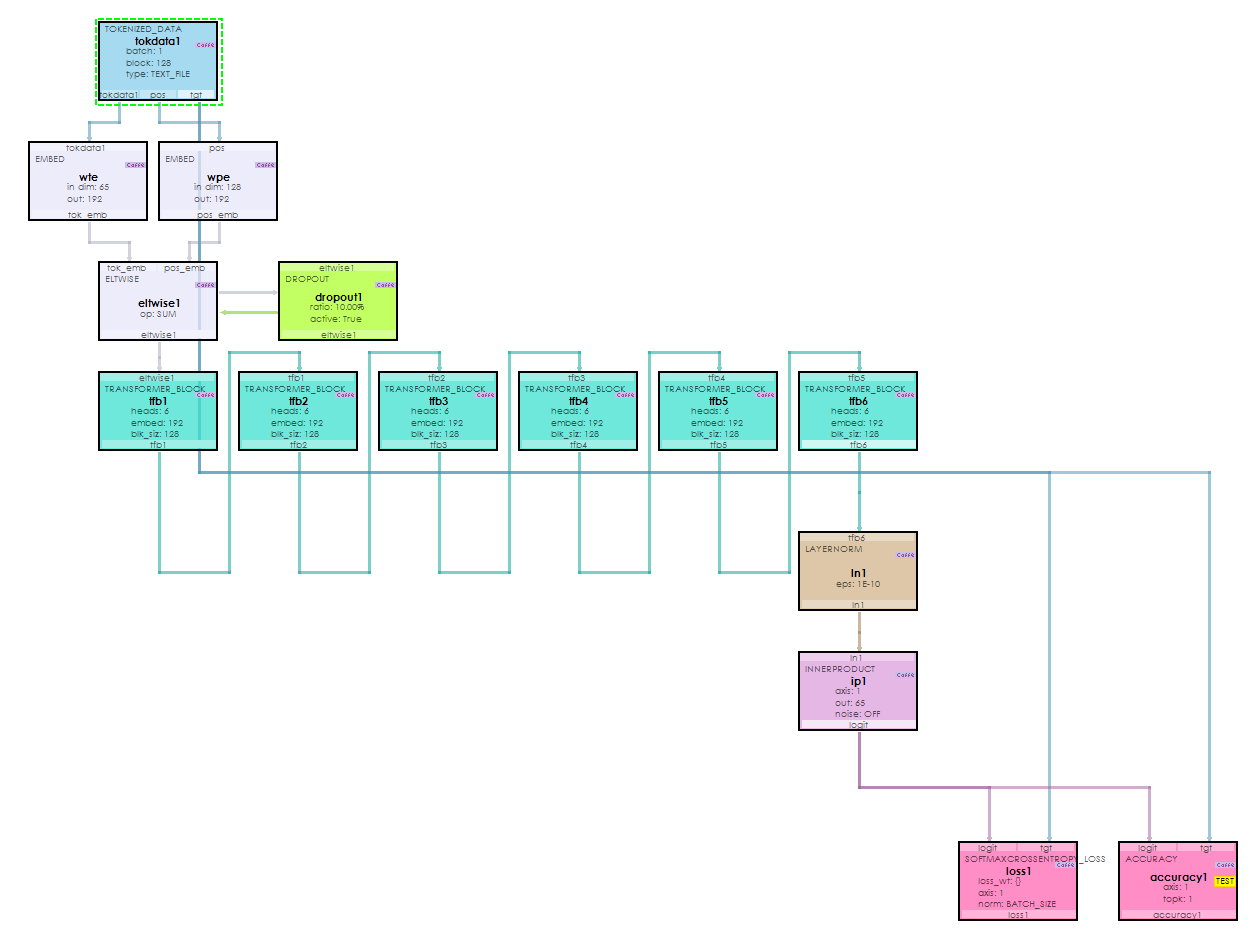
As you can see, the minGPT model feeds learned embeddings for both the token and position data into a stack of six TransformerBlockLayers, which are normalized and ultimately fed to an InnerProductLayer to create the logits. The logits are then fed through a SoftmaxLayer to produce the probability distribution for the next output based on the given input.
Inside each TransformerBlockLayer resides the CausalSelfAttentionLayer which is used to learn the context at the current transformer block. The output is normalized and fed through the MLP that includes the activation layer. Note, we use a RELU activation layer whereas the minGPT project (and other GPT models) use a GELU layer. We chose the RELU activation for its curve is close to the GELU and the observed results were very similar.
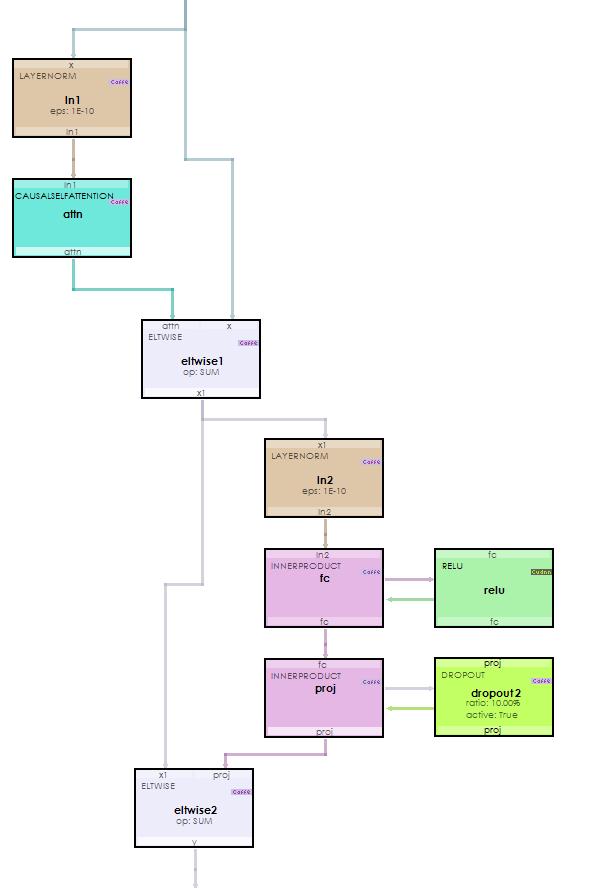
At the end of the GPT model, a SoftmaxCrossEntropyLoss layer computes the loss. One difference that you will note when viewing the MyCaffe GitHub implementation of the new classes is that we not only compute the forward pass, but also compute the gradient calculations of the backward pass for MyCaffe uses direct gradient calculations, thus giving you the developer more fine-grained control over and access to the gradient calculations.
GPT MyCaffe Model Results
When running the MyCaffe minGPT model on a Shakespeare sonnet, the model produces the following results after 2200 iterations.
You: O God! O God! Robot: hath men are wise friends, Becomes for him, we thing have stands to this brother's To do my blanchings and so my father's Before my perish, thy possite and seems depart. HERRY BOLINGBROKE: Thence two some a suffer, we my circuptanly: And what will they have no farthy too. PRINCE EDWARD: O, I hope some these swords, still me, they would With that do me to the service? BUCKINGHAM: No, that, ha, and they married, at my drums Is not my fortune world too too: They my father word,--look their princess! And how, madam, for thee will never by, Her and their courageous whiper of him. GLOUCESTER: The wreck that this but sweet with sitters with My fortune and so with him divine made, Thy household and thee they was deted on his groans To be ass, as he hath made trim to love our tongue. And see me, be touchefute for me, Thy tomble proportion or are together worse. Whrat you, we would help you shalt peer, your to be conceive in that is my fight of his daughters. Fellow, how my mistractial In all the same propency faulty forbilit The fiendly wind of panished woe. And her to distal possible and tell up, And let him her and my successe steed To him on the fearfulling, To black the firry wondering, if as thing be The complain with so some others of double them To the stumble my body well. SICINIUS: No, for well, will you hunt, The band somer pettiting in your good himself. CORIOLANUS: We can have, sir and all thou been my master. BRUTUS: Younders, saw we speaks, and all all Brief a thremity. Sirrah: Why not you do? MARCIUS: O think-mover! Where are your mother's command, To mend your friends? Come, madam, I have been Hear your foar worships and something How I may see you, take me to speak. ProffORO: Belovier you, sir! They shall demare, well nor her fears, I care it for him, and some what your matters? BAPTISTA: Sit my looks. HENRY BOLINGBROKE: And I am your swords? PROSPERO: No, to your hand.
To get even better results, just train for around 10k iterations.
GPT MyCaffe Implementation
To see the implementation of the new classes used in the GPT model, check them out on the MyCaffe GitHub site:
TokenizedDataLayer
TransformerBlockLayer
CausalSelfAttentionLayer
LayerNormLayer
SoftmaxCrossEntropy2LossLayer
New Features
The following new features have been added to this release.
- CUDA 11.8.0.522/cuDNN 8.6.0.163/nvapi 510/driver 522.06
- Windows 11 22H2
- Windows 10 22H2, OS Build 19045.2251, SDK 10.0.19041.0
- Added new LayerNormLayer
- Added new TransformerBlockLayer
- Added new TokenizedDataLayer
- Added new SoftmaxCrossEntropy2LossLayer.
- Added new AdamWSolver.
Bug Fixes
The following bugs have been fixed in this release.
- Fixed bug in TransposeLayer backward
- Fixed bug in SoftmaxCrossEntropyLoss layer when axis > 1
- Fixed bug in create run net with SoftmaxCrossEntropyLoss not converting.
To create and train your own GPT project to learn Shakespeare, check out the new Create and Train a GPT model to learn Shakespeare tutorial. For other great examples, including beating ATARI Pong, check out our Examples page.
Happy Deep Learning!
[1] Andrej Karpathy GitHub: karpathy/minGPT, 2022, GitHub
[2] Ilya Loshchilov, Frank Hutter Decoupled Weight Decay Regularization, 2017, 2019, arXiv:1711.05101

