Our last few posts on the Closed-form continuous-time (CfC) Liquid Neural Networks as described by [1], [2] and [3], have focused on learning to detect the last value in the input sequence.
In this post, we focus on detecting multiple values where the previous 82 values of a curve are used to detect the next 25 values.
NOTE: Originally we described this test as predicting the next 25 values, which is not correct for to actually predict future values, those values should be unknown and not exposed to the model during training. In our test here the 25 values following the input values are used in the optimizer step which trains one cycle (forward/backward) and uses the 25 values as the targets during that step to learn the dynamics of the curve. In this sample, the model detects the 25 values following the inputs but does not predict 25 unknown, never seen before, future values.
For each of our demonstrations we use the same simple Liquid Closed-form continuous-time Model as shown below.
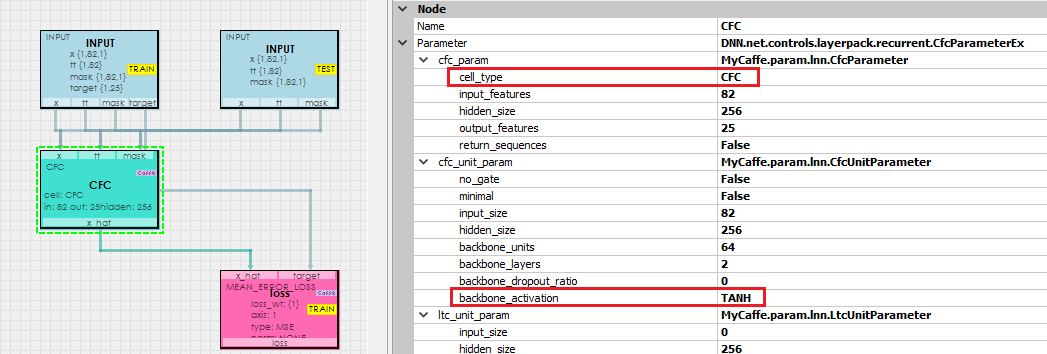
Note, our configuration of the CFC Layer uses the cell_type = CFC, which directs the layer to use an internal CfC Unit Layer. The CfC Unit Layer is configured to use the TANH activation function.
Detecting Multiple Values on a Sine Curve
Our first example focuses on detecting multiple values of a simple Sine curve.
As demonstrated in the video above, the CfC’s multiple detections track the Sine curve very quickly.
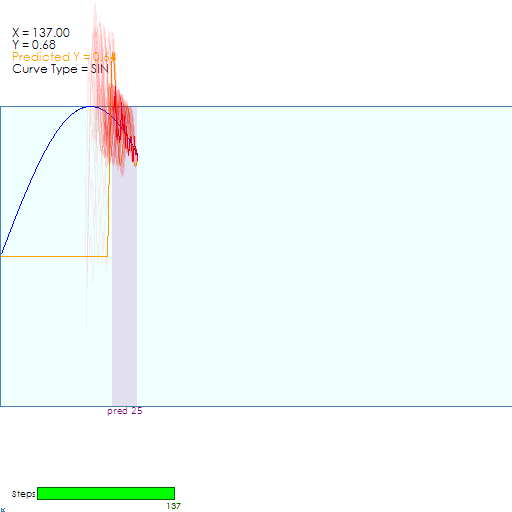
During the first steps the multiple detections are a jumbled mess, but quickly lock onto the curve as shown below.
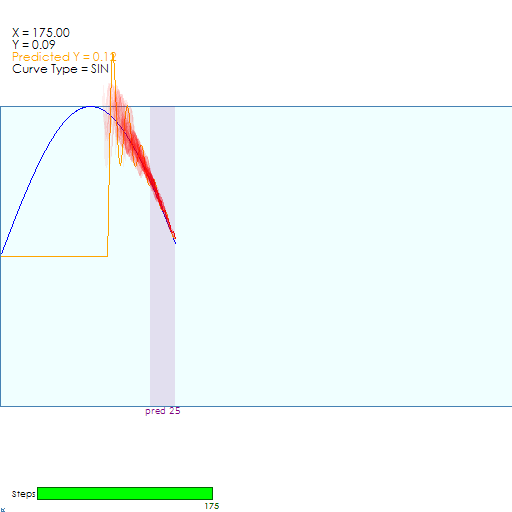
And once locked on, all detected values stay locked on for the duration.
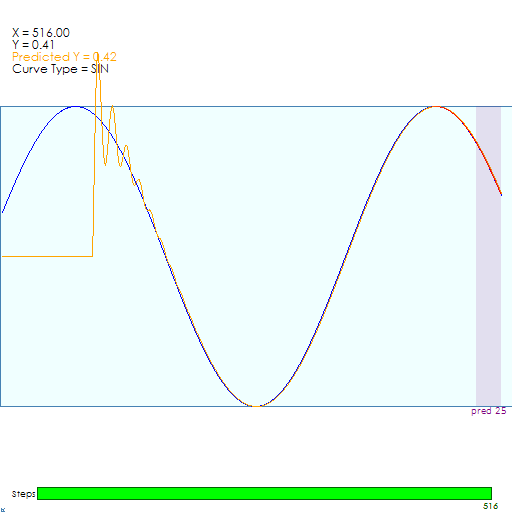
Admittedly, detecting the Sine curve is straightforward as the curve has a very periodic shape. Next, explore how detecting multiple values of the CfC work on a much more difficult curve.
Detecting Multiple Values on a Random Curve
Now this example may sound silly, but we want to see how well the CfC locks onto a cumulative set of random numbers by creating a curve with the following function:
α and β are each random numbers within the range [0.0, 1.0] and the overall curve is bound to the range [-1.0, 1.0]. Our intent with this test is to see how fast the CfC can lock onto and track the curve if at all.
As shown above, the CfC does a fairly good job of following and at least staying near the randomly generated curve! Similar to predicting the Sine curve, the first detections are a jumbled mess.
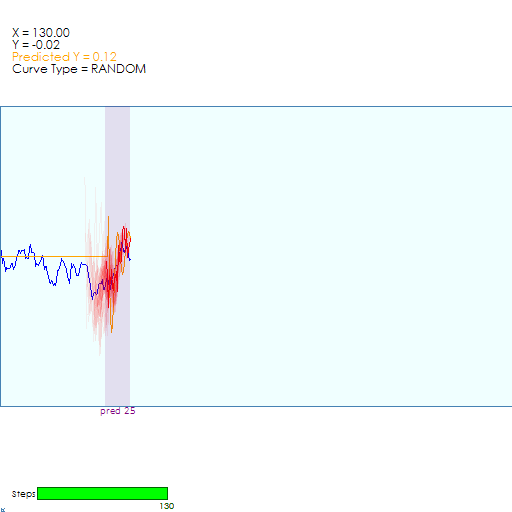
But after a short time, the multiple detections do start to organize and servo toward the random curve as a group.
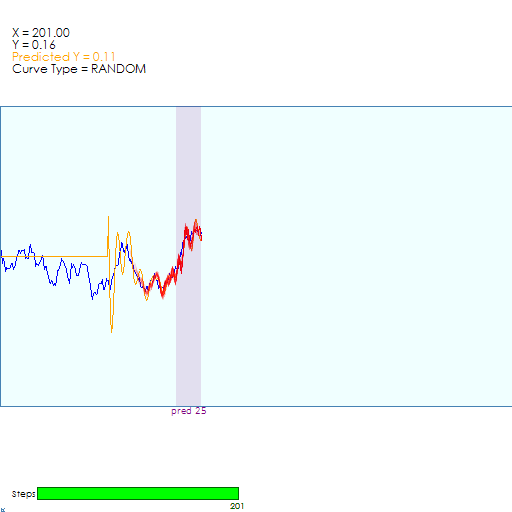
When the dynamics change dramatically, the servoing increases as the CfC attempts to find the best curve fit.
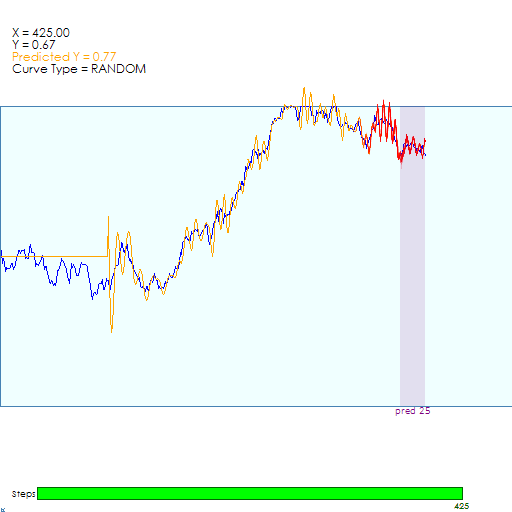
The way the CfC tracks a random curve really shows the power of these models! To read more about how this works, see our blog post Closed-form Continuous-time Liquid Neural Net Models – A Programmer’s Perspective.
To dig into the source code for this post, see the TestTrainingRealTimeFuture function on the MyCaffe GitHub site.
Happy Deep Learning with MyCaffe and Liquid CfC Neural Networks!
[1] Closed-form Continuous-time Neural Models, by Ramin Hasani, Mathias Lechner, Alexander Amini, Lucas Liebenwein, Aaron Ray, Max Tschaikowski, Gerald Teschl, Daniela Rus, 2021, arXiv:2106.13898
[2] Closed-form continuous-time neural networks, by Ramin Hasani, Mathias Lechner, Alexander Amini, Lucas Liebenwein, Aaron Ray, Max Tschaikowski, Gerald Teschl, Daniela Rus, 2022, nature machine intelligence
[3] GitHub: Closed-form Continuous-time Models, by Ramin Hasani, 2021, GitHub

